TinySpline

TinySpline is a small, yet powerful library for interpolating, transforming, and querying arbitrary NURBS, B-Splines, and Bézier curves. The core of the library is written in ANSI C (C89) with a C++ wrapper for an object-oriented programming model. Based on the C++ wrapper, auto-generated bindings for C#, D, Go, Java, Javascript, Lua, Octave, PHP, Python, R, and Ruby are provided.

Table of Contents

• License
• Features
• Installation
  • Pre-built Binaries
  • Compiling From Source
• Getting Started
• Documentation
• Publications
• Theoretical Backgrounds

License

MIT License - see the LICENSE file in the source distribution.

Features

• Object-oriented programming model
• B-Splines of any degree and dimensionality
• Spline interpolation
  • Cubic natural
  • Centripetal Catmull–Rom
• Evaluation
  • Knots
  • Sampling (multiple knots at once)
  • Equidistant points
  • Components (find y for given x)
• Reparametrization by arc length
  • Mapping length <--> knot
• Knot insertion (refinement)
• Sub-spline extraction
• Bézier curve decomposition
  • (also known as subdivision)
• Derivative
• Degree elevation
• Computation of rotation minimizing frames
• Morphing
• Serialization (JSON)
• Vector math

Installation

Pre-built Binaries

Releases can be downloaded from the releases page. In addition, the following package manager are supported:

Conan (C/C++):
https://conan.io/center/tinyspline

NuGet (C#):

<PackageReference Include="tinyspline" Version="0.6.0.1" />

Go:

go get github.com/tinyspline/go@v0.6.0

Luarocks (Lua):

luarocks install --server=https://tinyspline.github.io/lua tinyspline

Maven (Java):

<dependency>
   <groupId>org.tinyspline</groupId>
   <artifactId>tinyspline</artifactId>
   <version>0.6.0-1</version>
</dependency>

PyPI (Python):

python -m pip install tinyspline

RubyGems (Ruby):

gem install tinyspline

Compiling From Source

See BUILD.md.

Getting Started

A variety of examples (tests) can be found in the [test](test) subdirectory.

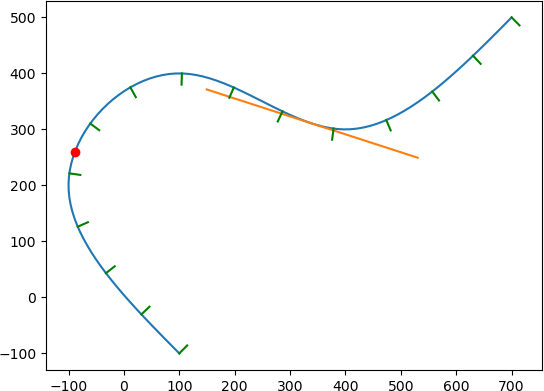
The following listing shows a Python example:

from tinyspline import *
import matplotlib.pyplot as plt
 
spline = BSpline.interpolate_cubic_natural(
  [
     100, -100, # P1
    -100,  200, # P2
     100,  400, # P3
     400,  300, # P4
     700,  500  # P5
  ], 2) # <- dimensionality of the points
 
# Draw spline as polyline.
points = spline.sample(100)
x = points[0::2]
y = points[1::2]
plt.plot(x, y)
 
# Draw point at knot 0.3.
vec2 = spline.eval(0.3).result_vec2()
plt.plot(vec2.x, vec2.y, 'ro')
 
# Draw tangent at knot 0.7.
pos = spline(0.7).result_vec2() # operator () -> eval
der = spline.derive()(0.7).result_vec2().normalize() * 200
s = pos - der
t = pos + der
plt.plot([s.x, t.x], [s.y, t.y])
 
# Draw 15 normals with equidistant distribution.
knots = spline.equidistant_knot_seq(15)
frames = spline.compute_rmf(knots)
for i in range(frames.size()):
    pos = frames.at(i).position
    nor = pos + frames.at(i).normal * 20
    # You can also fetch the tangent and binormal:
    #     frames.at(i).tangent
    #     frames.at(i).binormal
    plt.plot([pos.x, nor.x], [pos.y, nor.y], 'g')
 
plt.show()

Result:

Documentation

The latest Doxygen documentation can be found at: https://msteinbeck.github.io/tinyspline/

The documentation of the C interface (https://msteinbeck.github.io/tinyspline/tinyspline_8h.html) is quite extensive and also serves as an entry point for the C++ interface documentation (as well as the documentation for the bindings created from the C++ interface).

Publications

If you use TinySpline in your research, please cite it as below.

@INPROCEEDINGS{Steinbeck:SANER:21,
  author =       {Steinbeck, Marcel and Koschke, Rainer},
  booktitle =    {2021 IEEE International Conference on Software
                  Analysis, Evolution and Reengineering (SANER)},
  title =        {TinySpline: A Small, yet Powerful Library for
                  Interpolating, Transforming, and Querying NURBS,
                  B-Splines, and Bézier Curves},
  year =         {2021},
  pages =        {572-576},
  doi =          {10.1109/SANER50967.2021.00068}
}

Other publications:

@INPROCEEDINGS{Steinbeck:VISSOFT:22,
  author =       {Steinbeck, Marcel and Koschke, Rainer},
  booktitle =    {2022 Working Conference on Software Visualization
                  (VISSOFT)},
  title =        {Edge Animation in Software Visualization},
  year =         {2022},
  pages =        {63-74},
  doi =          {10.1109/VISSOFT55257.2022.00015}
}

Theoretical Backgrounds

[1] is a very good starting point for B-Splines.

[2] explains De Boor's Algorithm and gives some pseudo code.

[3] provides a good overview of NURBS with some mathematical background.

[4] is useful if you want to use NURBS in TinySpline.